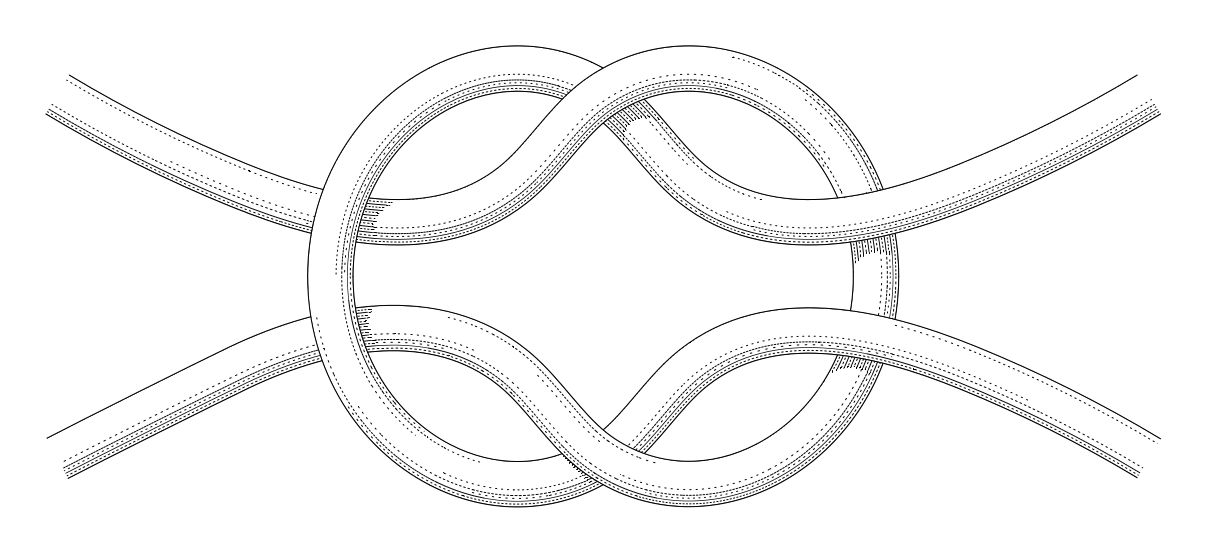
My field of study is geometric topology. I am interested in geometric objects up to dimension 4 and their embeddings. In particular, I study knots and their mathematical properties. Here is an example of an interesting (part of a) knot:

I am especially curious about concordance, a special equivalence relation on knots. This relation is intimately tied to questions on the topology of 4-manifolds and their smooth structures.
An introduction to the basic notions and tools of geometric topology with a special focus on three dimensional manifolds.
G26.5, Fridays 11:15
We will go through the book of Freed and Uhlenbeck, and learn about Instantons and 4-manifolds and the involved analysis. This will culminate in a proof of Donaldson's diagonalisation theorem.
H312, Fridays 11:15
Introduction to linear algebra for engineers. We cover linear independence, dimension, determinants, eigenvalues, diagonalisation, and complex numbers.
After recalling why light bulbs are standard in dimension 3, we go through Gabai's proof (ArXiv:1705.09989) of the corresponding statement in dimension 4. Along the way, we pick up the necessary background on embedded Morse theory and diffeomorphism groups.
H312, Fridays 13:00
Introduction to algebraic topology with focus on the fundamental group and homology.
We study the approach to Seiberg-Witten theory of Bauer-Furuta using stable homotopy theory.
Introduction to linear algebra with applications from probability theory and optimisation.
Complex calculus focusing on methods for evaluating integrals over domains in the complex plane and the computation of various transforms and their application in engineering.